The Transformation Problem (2016)

What follows is an unusually long and math-heavy essay compared to other writing on RedSails; not coincidentally, it’s also the first time we’ve had to render math by implementing $LATEX$. ^[1] In our opinion the effort is worth it — the transformation problem has dogged Marxism for long enough, and we do not want our readers to be caught by surprise when neoclassical economists (or worse, other Marxists) throw it in their faces.

The political stakes are straightforward: Marxism ceases to be Marxism when it bails on the labor theory of value. Intellectually, Wright’s research opens the door to further investigations of the fault line between capitalist and natural necessity running through economic thought and modeling. ^[2] [3] It is our hope that further work in this direction will be able to expose more and more concrete ways in which capitalist social arrangements, despite their seeming necessity, are ultimately irrational and superable.
 — N. F.

---

Contents

• RS Preface
• Introduction
• 1. The definition of “labour value”
• 2. Ricardo’s problem of an invariable measure of value
• 3. Marx’s transformation problem
• 4. Total labour costs
• 5. Capitalist households
• 6. The divergence of technical and total labour costs
• 7. Total labour costs: super-integrated labour values
• 8. The category-mistake: conflating technical and total labour costs
• 9. Dissolution of the problem of an invariable measure of value
• 10. Dissolution of the transformation problem
• Conclusion
• References

RS Preface

The transformation problem has provoked controversy within Marxism and derision from without for more than a century. Bourgeois economists in particular (beginning with Ladislaus Bortkiewicz, and continuing, most notoriously, with Paul Samuelson) have seized on it to argue for the basic inconsistency or vacuousness of Marx’s labor theory of value. Some Marxists consider these arguments so damning that they’ve abandoned the labor theory of value (as in the case of most analytical Marxists) or chosen to call any empirically verifiable version of it non-Marxian (as in the case of the value-form theorists). Without the labor theory of value, the critique of capitalism becomes an abstract ought, unmoored from its class partisanship and divorced from the scientific analysis of capitalist society. But the transformation problem can trouble those who accept the labor theory of value too. Marxists remain divided over how it should be handled, how close Marx came to solving it, what it means, and to what extent it matters.

The problem itself is simple enough to understand, and Marx was aware of it: if labor is the source of all value, then the labor values of commodities can be understood as sums of direct labor and indirect labor (that is, commodity inputs). The proportion between the two will, in general, vary, and this fact (the varying organic composition of capital across industries) is hard to square with the assumption of a uniform profit rate ^[4], if direct labor alone is the source of surplus value. Prices must evidently diverge from these “pure” labor values to get a uniform rate of profit, and the challenge for the labor theory of value is to show that embodied labor still governs these prices, that is, that values cannot be considered superfluous and deprecated in favor of a subjective view of price as only expressing supply and demand (as neoclassical economics would have it). The transformation problem, then, is the question of whether any lawful “transformation” between values and prices exists.

Ian Wright’s solution/dissolution of the transformation problem is the clearest and most conclusive response I have come across. This essay is the key second chapter of his doctoral dissertation, ^[5] also available as an earlier, stand-alone journal publication. ^[6] Wright does not reject either the linear production modeling approach or the uniform profit rate assumption of Marx’s neoclassical (and leftist!) critics. Instead he calls attention to historically specific capitalist social costs that are omitted from the traditional labor-value calculations. His concept of “super-integrated labour-values” is invaluable, even if the term itself is a little clunky. ^[7] In the seventh chapter of Wright’s thesis he presents a nonlinear dynamic model of classical macrodynamics which gives a plausible account of the “process by which the nominal and real cost structures of the economy grope toward a state of mutual consistency”. ^[8]

The takeaway from Wright’s thesis is two-sided. Marx and subsequent Marxists are found guilty of “a category error”, and the “causal claim [traditionally associated with the labor theory of value] — that labour costs are the sole cause or regulator of natural prices — does not generalise beyond simple commodity production”. More importantly, though, Wright’s finding “undermines the basis for the claim that a labour theory of value must be logically incoherent because prices and classical labour-values are quantitatively incommensurable in linear production models”, and upholds “the semantic claim [traditionally associated with the labor theory of value] — that classical gravitation establishes a lawful relationship between natural prices and labour costs” even beyond simple commodity production. The transformation problem, it turns out, derives from a fundamental tension not only in Capital but in all of Marxism ^[9] between the view from within capitalism and the view from without, between social laws and natural laws, between explaining what is and advocating what ought to be.

 — Nia Frome, December 2023.

---

Introduction

David Ricardo defines “natural prices” as stable exchange ratios that are independent of “accidental and temporary deviations” (Ricardo, [1817] 1996, p. 109) between supply and demand. And he defines reproducible commodities as those “that may be multiplied … almost without any assignable limit, if we are disposed to bestow the labour necessary to obtain them” (Ricardo, [1817] 1996, p. 59). Ricardo (2005a) observed that the natural prices of reproducible commodities vary with the distribution of income whereas their real costs of production, measured in labour time, do not. In consequence, labour costs cannot fully explain the structure of natural prices. This explanatory gap creates two famous problems in the classical labour theory of value: Ricardo’s problem of an invariable measure of value and Karl Marx’s transformation problem. These problems are the major reason why modern economists consider the classical labour theory of value as, at best, incomplete, or worse, logically incoherent (e.g., Seton, 1957; Samuelson, 1971; Lippi, 1979; Steedman, 1981).

Nonetheless, dissatisfaction with economic foundations based on the “shallow and superficial framework of supply and demand concepts” (Foley, 2000, p. 2) has ensured a continued interest in the classical problems. Despite significant intellectual effort, however, the classical problems remain essentially insoluble (see Howard and King, 1989, chapter 2; Howard and King, 1992, chapter 14).

For “ordinary language philosophers” (Passmore, 1978, chapter 18), such as Gilbert Ryle ([1949] 1984) and Ludwig Wittgenstein (1953), the underlying cause of a long-lived and insoluble problem is often a hidden conceptual confusion or mistake. The problem is insoluble because the conceptual framework in which the problem is stated is itself faulty. The problem must therefore be deflated or dissolved by applying “conceptual analysis” (Sloman, 1978, chapter 4).

For instance, Ryle introduced the term “category-mistake” (Ryle, [1949] 1984, chapter 1) to denote the conceptual error of expecting some concept or thing to possess properties it cannot have. For example, John Doe may be a relative, friend, enemy or stranger to Richard Roe; but he cannot be any of these things to the “Average Taxpayer”. So if “John Doe continues to think of the Average Taxpayer as a fellow-citizen, he will tend to think of him as an elusive an insubstantial man, a ghost who is everywhere yet nowhere” (Ryle, [1949] 1984, p. 18).

The argument of this essay is that the contradictions of the classical labour theory of value derive from a “theoretically interesting category-mistake” (Ryle, [1949] 1984, p. 19), specifically the mistake of supposing that classical labour-values, which measure strictly technical costs of production, are of the same logical type as natural prices, which measure social costs of production, and in consequence labour-values and prices, under appropriate equilibrium conditions, are mutually consistent. Since this supposition is mistaken, Ricardo’s search for an invariable measure of value and Marx’s search for a transformation between labour-values and prices, attempt to discover a commensurate relationship between concepts defined by incommensurate cost accounting conventions. They therefore seek an “elusive and insubstantial man” or “ghost”.

The identification of a category-mistake allows a resolution of the classical problems by “giving prominence to distinctions which our ordinary forms of language make us easily overlook” (Wittgenstein, 1953, § 132). ^[10] Such distinctions can then solve, or more accurately, dissolve the problems.

This chapter therefore introduces a new distinction, lacking in the classical labour theory, between a “technical” and a “total” measure of labour cost, where technical labour cost corresponds to the classical concept and total labour cost includes additional real costs of production incurred in virtue of non-technical, or social, conditions of production, such as production financed by a capitalist class. The more refined conceptual framework separates theoretical concerns that are conflated in the classical theory. For example, labour-values apply to distribution-independent questions about an economy, such as the productivity of labour over time or the quantity of “surplus labour” supplied by workers to capitalists (i.e., technical issues or questions in the theory of labour exploitation), whereas total labour-values apply to distribution-dependent questions, such as the relationship between nominal prices and the actual labour time required to produce commodities (i.e., issues in the theory of economic value). The classical problems dissolve by generalising the classical labour theory to apply both concepts of labour cost in the appropriate contexts. In consequence, I sketch, in an initial and incomplete manner, a new theoretical object: a more general labour theory of value with an invariable measure of value and without a transformation problem.

The structure of this chapter is as follows. The next three sections specify how the classical problems manifest in the simplest possible case — that of a capitalist economy in steady-state equilibrium. The subsequent section then introduces the concept of a “total labour cost”, in contradistinction to the classical concept, by applying conceptual analysis to the concept “labour-value”. The following three sections formally define total labour costs in the case of steady-state equilibrium. The final three sections explain how the new distinction dissolves the classical problems.

1. The definition of “labour value”

Since the seminal contribution of Ladislaus von Bortkiewicz ([1907] 1975), the transformation problem is normally defined in terms of properties of simultaneous equations. ^[11] I therefore begin by translating the classical concept of “labour value” into linear production theory (e.g., see Kurz and Salvadori, 1995). The formality imparts precise semantics to our key concepts, which helps identify the conceptual mistake.

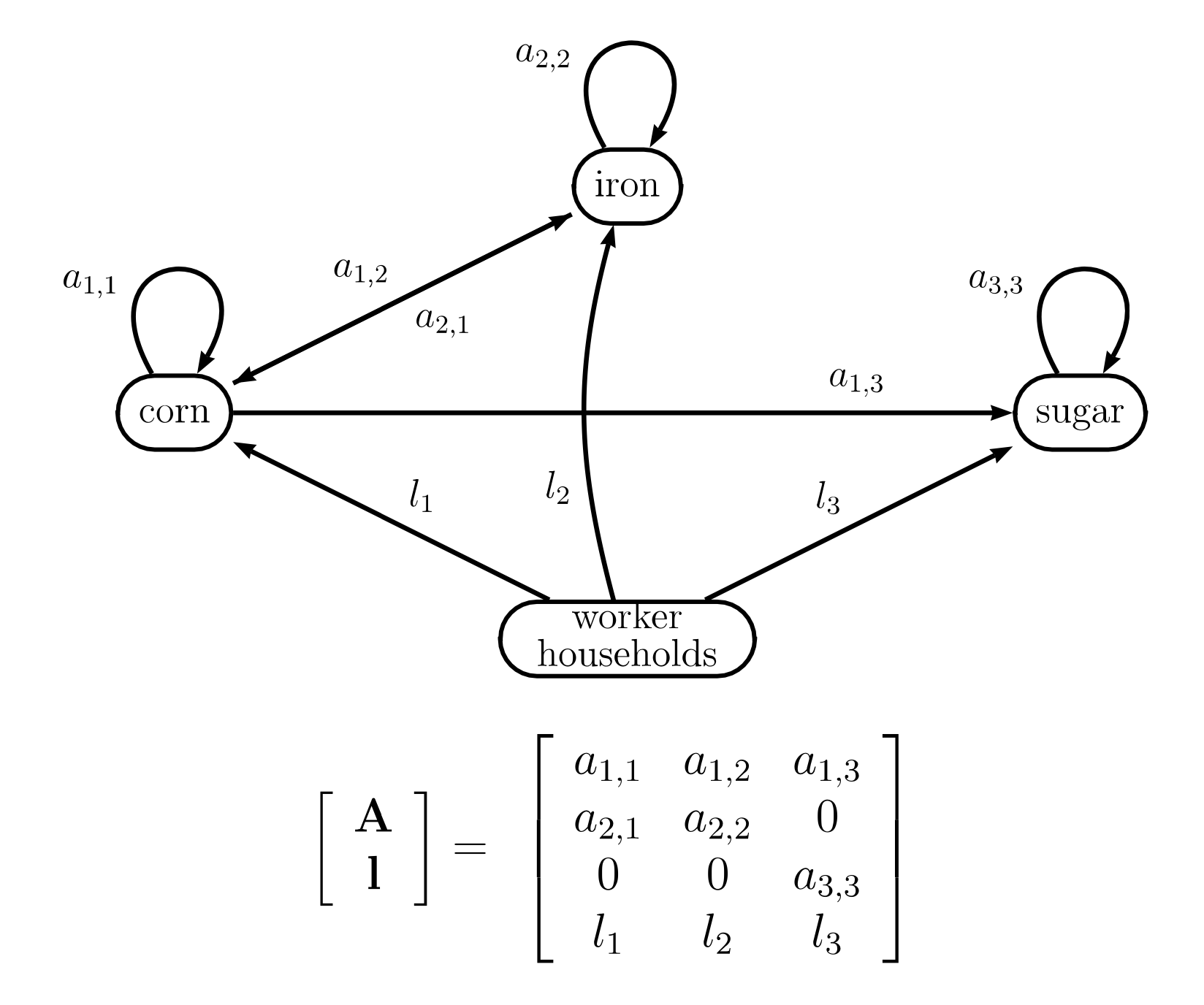
Assume $n\in {\mathbb{Z}}^{+}$ sectors that specialise in the production of one commodity type. The technique is a non-negative $n\times n$ input-output matrix of inter-sector coefficients, $\mathbf{A}=[a_{i,j}]$. Each $a_{i,j}\ge 0$ is the quantity of commodity $i$ directly required to produce one unit of commodity $j$. Assume (i) $\mathbf{A}$ is fully connected, (ii) $\mathbf{I}-\mathbf{A}$ is of full rank and (iii) there exists a row vector ^[12], $\mathbf{x}\in {ℝ}_{+}^n$, such that $\mathbf{x}>\mathbf{A}\mathbf{x}$, i.e. the technique is productive. The $1\times n$ vector, $\mathbf{l}=[l_i]$, are direct labour coefficients, where each $l_i>0$ is the quantity of labour directly required to output 1 unit of commodity $i$. Figure 1 depicts an example three-sector technique both as a matrix and weighted directed graph.

Fig 1: A technique for an example 3-sector economy depicted as a directed graph and a matrix.

The total “coexisting labour” (see Hodgskin, 1825; Marx, 2000, chapter 21, section 3; Perelman, 1987, chapter 5) supplied to reproduce commodity i is the direct labour operating in sector i plus the indirect labour operating in other sectors of the economy that is simultaneously supplied, in parallel, to replace all the commodity inputs used-up during the production of 1 unit of commodity i.

Marx, following the Ricardian socialist, Thomas Hodgskin, illustrated the concept of “coexisting labour” by contrasting it to “antecedent labour”:

‘[Raw] cotton, yarn, fabric, are not only produced one after the other and from one another, but they are produced and reproduced simultaneously, alongside one another. What appears as the effect of antecedent labour, if one considers the production process of the individual commodity, presents itself at the same time as the effect of coexisting labour, if one considers the reproduction process of the commodity, that is, if one considers this production process in its continuous motion and in the entirety of its conditions, and not merely an isolated action or a limited part of it. There exists not only a cycle comprising various phases, but all the phases of the commodity are simultaneously produced in the various spheres and branches of production.’ ^[13]

Commodities vary in their “difficulty of production” (e.g., Ricardo [1817] 1996, p. 106) because they require different quantities of coexisting labour for their reproduction. The classical labour theory of value is founded on this objective cost property of commodities, i.e. their “labour-value”.

To calculate a labour-value we vertically integrate over the technique (e.g., Pasinetti 1980). For example, production of unit $i$ uses-up direct labour $l_i$ plus the bundle of input commodities ${\mathbf{A}}^{(i)}$ (i.e., column $i$ of matrix $\mathbf{A}$). This used-up input bundle is replaced by the simultaneous expenditure of indirect labour $\mathbf{l}{\mathbf{A}}^{(i)}$ operating in other sectors. But this production itself uses-up another bundle of input commodities $\mathbf{A}{\mathbf{A}}^{(i)}$, which is also replaced by the simultaneous expenditure of an additional amount of indirect labour $\mathbf{l}\mathbf{A}{\mathbf{A}}^{(i)}$. To count all the coexisting labour, $v_i$, we continue the sum; that is,

$$\begin{array}{cc}\hfill v_i& =l_i+\mathbf{l}{\mathbf{A}}^{(i)}+\mathbf{l}\mathbf{A}{\mathbf{A}}^{(i)}+\mathbf{l}{\mathbf{A}}^2{\mathbf{A}}^{(i)}+\dots \hfill \\ \hfill & =l_i+\mathbf{l}(\mathbf{I}+\mathbf{A}+{\mathbf{A}}^2+\dots ){\mathbf{A}}^{(i)}\hfill \\ \hfill & =l_i+\mathbf{l}({\sum }_{n=0}^{\infty }{\mathbf{A}}^n){\mathbf{A}}^{(i)}\text{.}\hfill & \hfill \text{(1)}\end{array}$$

This infinite sum converges since the technique is productive (see Lancaster, 1968, chapter 6). The vector of labour-values, from equation (1), is then

$$\mathbf{v}=\mathbf{l}+\mathbf{l}({\sum }_{n=0}^{\infty }{\mathbf{A}}^n)\mathbf{A}=\mathbf{l}{\sum }_{n=0}^{\infty }{\mathbf{A}}^n\text{.}$$

An alternative representation of the infinite series $\sum {\mathbf{A}}^n$ is the Leontief inverse $(\mathbf{I}-\mathbf{A}{)}^{-1}$. Hence, $\mathbf{v}=\mathbf{l}(\mathbf{I}-\mathbf{A}{)}^{-1}$; that is:

Definition 1. “Classical labour-values”, $\mathbf{v}$, are given by

$$\begin{array}{ccc}\hfill \mathbf{v}& =\mathbf{v}\mathbf{A}+\mathbf{l}\text{.}\hfill & \hfill \text{(2)}\end{array}$$

This equation was probably first written down by Dmitriev (1868-1913) who translated the classical concept of ‘labour embodied’ into a mathematical formula (Nuti, 1974; Dmitriev, 1974). Dmitriev’s formula is now standard (e.g., Sraffa 1960; Samuelson 1971; Pasinetti 1977; Steedman 1981).

Now we’ve defined labour-values let us turn to two famous contradictions of the classical labour theory of value.

2. Ricardo’s problem of an invariable measure of value

Consider a tree A that is twice the height of a tree B. At a later date tree A is three times the height of tree B. Assume we only know the relative change in heights. Does this change indicate that tree A has increased in size, tree B has decreased in size, or some combination of these causes? To answer this question we need an absolute measure of height that is invariable over time.

The “metre” is such an invariable standard. We measure the absolute height of tree A and B in metres, both before and after the change. Then we can unambiguously determine the cause of the variation in relative heights.

The definition and adoption of the metre by post-revolutionary France in 1793 was accompanied by much theoretical debate and reflection (Roncaglia, 2005, p. 192). Ricardo, a contemporary of these events, recognised that an objective theory of economic value requires an analogous invariable standard of measurement.

Market prices — whether stated in terms of exchange ratios between commodities or in terms of a money-commodity — cannot function as a standard because prices merely indicate relative values:

If for example a piece of cloth is now the value of 2 ounces of gold and was formerly the value of four I cannot positively say that the cloth is only half as valuable as before, because it is possible that the gold may be twice as valuable as before. (Ricardo, 2005a, p. 289)

The cause of an altered exchange ratio might be due to an alteration in the absolute value of the standard itself. Picking a market price to measure absolute value is analogous to picking the height of a specific tree to function as an invariable standard of length. Between measurements the chosen tree might grow (or get cut down in size).

Perhaps we shouldn’t try to find a standard? This is not an option because, lacking an invariable standard, the theory of value collapses into subjectivity, leaving “every one to chuse his own measure of value” (Ricardo, 2005a, p. 370). In consequence, public statements about objective value, such as “commodity A is now less valuable than one year ago”, would, strictly speaking, be nonsense.

Ricardo states that if we had “possession of the knowledge of the law which regulates the exchangeable-value of commodities, we should be only one step from the discovery of the measure of absolute value” (Ricardo, 2005b, p. 315). Ricardo therefore looks beyond exchange ratios in the marketplace to seek a regulating cause that might constitute a “standard in nature” (Ricardo, 2005a, p. 381).

Ricardo claims that the natural price of a reproducible commodity is regulated by its “difficulty of production” measured in labour time (e.g., Ricardo, [1817] 1996, chapter 4). In conditions of constant “difficulty of production” market prices gravitate toward or around their natural prices due to profit-seeking behaviour, which reallocates capital to high-profit sectors and away from low-profit sectors.

Such natural prices, or “prices of production” (Marx, [1894] 1971, ch. 9), are equilibrium prices with uniform profit-rates, which we can define as,

$$\begin{array}{ccc}\hfill \mathbf{p}& =(\mathbf{p}\mathbf{A}+\mathbf{l}w)(1+r)\text{,}\hfill & \hfill \text{(3)}\end{array}$$

where $\mathbf{p}$ is a vector of prices (measured, say, in pounds sterling), $w$ is a wage rate (pounds per hour), and $r$ is a uniform rate of profit or percentage interest-rate on the money invested to fund the period of production. Equation (3) states that the production price $p_i$ of commodity-type $i$ has three components: (i) the cost of the input bundle, $\mathbf{p}{\mathbf{A}}^{(i)}$, paid to other sectors of production, (ii) the wage costs, $l_{i}w$, paid to workers in sector $i$, and (iii) the profits, $(\mathbf{p}{\mathbf{A}}^{(i)}+l_{i}w)r$, received by capitalists, as owners of firms in this sector, on the money-capital they advance to pay input and direct labour costs (collectively, the cost-price).

Now if “difficulty of production”, measured in units of labour, in fact regulates natural prices then, in theory, we can measure (absolute) labour-values to unambiguously determine the cause of variations in (relative) prices. We would have identified a “standard in nature” and Ricardo could “speak of the variation of other things, without embarrassing myself on every occasion with the consideration of the possible alteration in the value of the medium in which price and value are estimated” (Ricardo, [1817] 1996, p. 80).

In fact, in some special cases labour-values do vary one-to-one with natural prices. For instance, Adam Smith [1776] (1994, p. 53) restricts the applicability of a labour theory of value to an “early and rude state of society” that precedes the “accumulation of stock”, where profits are absent and “the whole produce of labour belongs to the labourer”. In these circumstances a natural price is simply the wage bill of the total coexisting labour supplied to produce the commodity; that is,

Proposition 1. $r=0$ implies $\mathbf{p}=w\mathbf{v}$.

Proof. Set $r=0$ into price equation (3) to get $\mathbf{p}=\mathbf{p}\mathbf{A}+\mathbf{l}w$ or $\mathbf{p}=w\mathbf{l}(\mathbf{I}-\mathbf{A}{)}^{-1}$. Since $\mathbf{v}=\mathbf{l}(\mathbf{I}-\mathbf{A}{)}^{-1}$ the conclusion follows.

So prices are proportional to labour-values with constant of proportionality $w$. Hence (relative) prices vary one-to-one with (absolute) labour-values.

Ricardo notes that if the ratio of ‘fixed capital’ (i.e., the input bundle) to ‘circulating capital’ (i.e., the real wage bundle for “the support of labour”) is identical in all sectors then production prices are proportional to labour-values (Ricardo, [1817] 1996, p. 31). Define $\overline{\mathbf{w}}=(1/\mathbf{l}{\mathbf{q}}^{\text{T}})\mathbf{w}$ as the real wage bundle consumed per unit of labour supplied, where $\mathbf{q}=[q_i]$ is the scale of production or gross product. Then Ricardo’s ratio, in terms of labour-values, is

$$k=\frac{\mathbf{v}{\mathbf{A}}^{(i)}}{\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}{l}_i}\text{,}$$

where $\mathbf{v}{\mathbf{A}}^{(i)}$ is the labour-value of the input bundle and $\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}{l}_i$ is the labour-value of the real wage consumed by workers in sector $i$. Marx would later call this ratio the technical or organic “composition of capital” (Marx, [1894] 1971, Ch. 8). A uniform organic composition of capital implies price-value proportionality; that is,

Proposition 2. $\mathbf{v}\mathbf{A}=k\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}\mathbf{l}$ implies $\mathbf{p}=\alpha \mathbf{v}$, where $\alpha =w(1+r)/(1-k\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}r)$.

Proof. Write price equation (3) in series form:

$$\begin{array}{cc}\hfill \mathbf{p}& =(\mathbf{p}\mathbf{A}+\mathbf{l}w)(1+r)\hfill \\ \hfill & =w(1+r)\mathbf{l}(\mathbf{I}-\mathbf{A}(1+r){)}^{-1}\hfill \\ \hfill & =w(1+r)\mathbf{l}{\sum }_{n=0}^{\infty }{\mathbf{A}}^n(1+r{)}^n\text{.}\hfill \end{array}$$

Let $k^{\prime }=k\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}$. Given uniformity, $\mathbf{v}\mathbf{A}=k^{\prime }\mathbf{l}$, and therefore,

$$\begin{array}{ccc}\hfill \mathbf{p}& =w(1+r)\frac{1}{k^{\prime }}{\sum }_{n=0}^{\infty }\mathbf{v}{\mathbf{A}}^{n+1}(1+r{)}^n\text{.}\hfill & \hfill \text{(4)}\end{array}$$

Given uniformity and the definition of labour-value, $\mathbf{v}=\mathbf{v}\mathbf{A}+\mathbf{l}$, then $\mathbf{v}\mathbf{A}=(k^{\prime }/k^{\prime }+1)\mathbf{v}$. Hence $\mathbf{v}{\mathbf{A}}^2=(k^{\prime }/k^{\prime }+1)\mathbf{v}\mathbf{A}=(k^{\prime }/k^{\prime }+1{)}^2\mathbf{v}$ and by induction, $\mathbf{v}{\mathbf{A}}^n=(k^{\prime }/(k^{\prime }+1){)}^n\mathbf{v}$. Substitute into price equation (4) to get

$$\mathbf{p}=\left(w{\sum }_{n=0}^{\infty }\frac{(k^{\prime }{)}^n(1+r{)}^{n+1}}{(1+k^{\prime }{)}^{n+1}}\right)\mathbf{v}\text{.}$$

Given that $k^{\prime }r<1$ then the infinite sum converges to $(1+r)/(1-k^{\prime }r)$.

Proposition 2 confirms Ricardo’s thesis. Again, in these special circumstances, production prices vary in lock-step with labour-values. Ricardo therefore claims that “the quantity of labour bestowed on a commodity … is under many circumstances an invariable standard” (Ricardo, [1817] 1996, p. 19).

But apart from ‘many’ special cases there exists an infinite number of cases where production prices fail to vary one-to-one with labour-values. The reason is simple: production prices, $\mathbf{p}$, are a function of the profit-rate, $r$, but labour-values, $\mathbf{v}$, are not. Hence a variation in the profit-rate alters prices but leaves labour-values entirely unchanged. As Ricardo (2005a) clearly identifies: price depends on the distribution of income (i.e., how the net product is distributed in the form of wage and profit income) but “difficulty of production”, a purely technical measure of direct and indirect labour costs, does not; therefore, production prices have an additional degree-of-freedom unrelated to labour-values. In general, the relative value of a commodity varies independently of its absolute value.

This is very perplexing since it is analogous to discovering that the relative size of two trees can change even though their absolute sizes, measured in metres, remain unaltered. Such a discovery would imply the metre is not an invariable standard of size, or one’s theory of size is flawed. Ricardo’s problem of an invariable standard of value arises, therefore, because his labour theory of value cannot fully account for production prices. The profit component of price appears to be unrelated to any objective labour cost. Although “the great cause of the variation of commodities is the greater or less quantity of labour that may be necessary to produce them” there is another “less powerful cause of their variation” (Ricardo, 2005a, p. 404).

Ricardo understands the necessity for an invariable standard in his theoretical framework yet simultaneously understands the conditions that prevent this necessity from being met. Faced with a contradiction he is forced to draw the negative conclusion that there cannot be an invariable standard of value.

Now let us turn to a related problem in Marx’s theory of value.

3. Marx’s transformation problem

Marx ([1867] 1954) explicitly assumes prices are proportional to labour-values in Volumes I and Il of Capital. On this basis profit is the money representation of the unpaid or “surplus labour” of the working class. But Marx must establish the generality of this proposition in the case of (non-proportional) production prices. He tackles the issue in unfinished notes published as Volume III of Capital (Marx, [1894] 1971).

Marx proposes that aggregates of labour-values and production prices are proportional, even though individual prices and labour-values diverge, and therefore total profit remains the money representation of total surplus labour.

Let us reproduce Marx’s reasoning in terms of linear production theory. Define $\mathbf{q}=[q_i]$ as the scale of production or gross product and $\mathbf{w}=[w_i]$ as the real wage. The total labour supplied is therefore $\mathbf{l}{\mathbf{q}}^{\text{T}}$ and bundle $\overline{\mathbf{w}}=(1/\mathbf{l}{\mathbf{q}}^{\text{T}})\mathbf{w}$ is the real wage consumed per unit of labour supplied.

Marx defines the “surplus-labour” in sector $i$ as the labour supplied in excess of the labour-value of the real wage consumed, i.e. $l_i{q}_i-l_i{q}_i\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}$. The “rate of surplus-value”, or “degree of exploitation”, for sector $i$, is then the ratio of surplus-labour to the labour-value of the real wage. Marx assumes, for simplicity, that the degree of exploitation is uniform across sectors,

$$\theta =\frac{l_i{q}_i-l_i{q}_i\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}}{l_i{q}_i\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}}=\frac{1-\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}}{\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}}\text{.}$$

A high (resp. low) $\theta$ implies capitalists receive a larger (resp. smaller) share of the fruits of the labour they employ.

Now, according to Marx, only “living labour” creates profit from production. Hence the profit produced in each sector depends on the labour directly employed in that sector (the “variable capital”) but is independent of the scale and composition of the material inputs to that sector (the “constant capital”). What, then, is the profit-rate in each sector?

Marx considers an initial situation of prices proportional to labour-values. In these circumstances a sector’s profit-rate is the ratio of surplus-labour to the sum of the labour-value of constant and variable capitals,

$$\begin{array}{cc}\hfill r_i& =\frac{(1-\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}})l_i{q}_i}{\mathbf{v}{\mathbf{A}}^{(i)}{q}_i+\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}{l}_i{q}_i}\hfill \\ \hfill & =\theta \frac{1}{(\mathbf{v}{\mathbf{A}}^{(i)}/\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}{l}_i)+1}\text{.}\hfill \end{array}$$

In consequence, the profit-rates in each sector, $r_i$, are only equal if the “organic compositions” of capitals, that is the ratios $\mathbf{v}{\mathbf{A}}^{(i)}/\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}{l}_i$, are also all equal (Marx, [1867] 1954, chapter 25, section 1). But they are not equal; hence, “in the different spheres of production with the same degree of exploitation, we find considerably different rates of profit corresponding to the different organic composition of these capitals” (Marx, [1894] 1971, p. 155).

Marx notes that his initial situation is unstable: “The rates of profit prevailing in the various branches of production are originally very different” (Marx, [1894] 1971, p. 158) but, during the formation of production prices, the different rates “are equalised by competition to a single general [uniform] rate of profit” (Marx, [1894] 1971, p. 158).

Marx proposes that production prices conservatively redistribute the surplus-labour amongst capitalist owners (in the form of commodities purchased with profit income), at which point, “although in selling their commodities the capitalists of various spheres of production recover the value of the capital consumed in their production, they do not secure the surplus-value [i.e., surplus-labour], and consequently the profit, created in their own sphere by the production of these commodities.” (Marx, [1894] 1971, p. 158). The capitalists share the available pool of surplus-labour in proportion to the size of the money-capitals they advance rather than the size of the (value-creating) workforces they employ.

Marx provides numerical examples to demonstrate the redistribution of surplus-value. He computes a uniform (labour-value) profit-rate, $r_v$, by dividing the aggregate surplus-labour by the aggregate labour-value of constant and variable capital,

$$\begin{array}{ccc}\hfill r_v& =\frac{(1-\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}})\mathbf{l}{\mathbf{q}}^{\text{T}}}{\mathbf{v}\mathbf{A}{\mathbf{q}}^{\text{T}}+\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}\mathbf{l}{\mathbf{q}}^{\text{T}}}\text{.}\hfill & \hfill \text{(5)}\end{array}$$

Marx states that the (labour-value) profit-rate, $r_v$, is identical to the uniform (money) profit-rate, $r$, which obtains once production prices have formed. He defines ‘prices of production’ as the initial cost-price of a commodity, which is proportional to labour-value, marked-up by the uniform profit-rate, $r_v$. Let $\alpha$ be the constant of proportionality. Then we can write Marx’s production prices as

$$\begin{array}{ccc}\hfill {\mathbf{p}}^{\star }& =\alpha (\mathbf{v}\mathbf{A}+\mathbf{l}(\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}))(1+r_v)\text{.}\hfill & \hfill \text{(6)}\end{array}$$

“Hence, the price of production of a commodity is equal to its cost-price plus the profit, allotted to it in per cent, in accordance with the general rate of profit, or, in other words, to its cost-price plus the average profit [i.e., $r_v$]” (Marx, [1894] 1971, p. 157).

Marx’s production prices ${\mathbf{p}}^{\star }$ are not proportional to labour-values. So “one portion of the commodities is sold above its [labour-]value in the same proportion in which the other is sold below it. And it is only the sale of the commodities at such prices that enables the rate of profit for capitals [to be uniform], regardless of their different organic composition” (Marx, [1894] 1971, p. 157).

In Marx’s view production prices scramble and obscure the source of profit in surplus-labour. But the labour theory of value continues to hold in the aggregate because the “transformation” from unequal profit-rates to production prices is conservative. Nominal price changes neither create nor destroy surplus-labour, but merely redistribute it.

Marx therefore claims that three aggregate equalities are invariant over the transformation: (i) the (money) profit-rate, $r$, is equal to the (labour-value) profit-rate, $r_v$; (ii) “the sum of the profits in all spheres of production must equal the sum of the surplus-values”, (Marx, [1894] 1971, p. 173); and (iii) “the sum of the prices of production of the total social product equal the sum of its [labour-]value” (Marx, [1894] 1971, p. 173) (here Marx assumes, for simplicity, that $\alpha =1$).

And in fact these equalities hold. Marx’s ‘prices of production’ are computed from the assumption that money and labour-value profit-rates are equal and therefore equality (i) is true by definition. Also, Marx’s prices ${\mathbf{p}}^{\star }$ satisfy equalities (ii) and (iii):

Proposition 3. Marx’s ‘production prices’, ${\mathbf{p}}^{\star }$, satisfy (ii) the sum of profits is proportional to surplus labour, $\alpha (\mathbf{v}\mathbf{A}+\mathbf{l}(\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}})){\mathbf{q}}^{\text{T}}r\propto \mathbf{l}{\mathbf{q}}^{\text{T}}-\mathbf{v}{\mathbf{w}}^{\text{T}}$, and (iii) the price of the gross product is proportional to its labour-value, ${\mathbf{p}}^{\star }{\mathbf{q}}^{\text{T}}\propto \mathbf{v}{\mathbf{q}}^{\text{T}}$.

Proof. Marx defines $r=r_v$. From equation (5), $(\mathbf{v}\mathbf{A}{\mathbf{q}}^{\text{T}}+\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}\mathbf{l}{\mathbf{q}}^{\text{T}})r=(1-\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}})\mathbf{l}{\mathbf{q}}^{\text{T}}=\mathbf{l}{\mathbf{q}}^{\text{T}}-\mathbf{v}{\mathbf{w}}^{\text{T}}$ (since $\overline{\mathbf{w}}=(1/\mathbf{l}{\mathbf{q}}^{\text{T}})\mathbf{w}$), which establishes (ii). Multiply equation (6) by $\mathbf{q}$ to yield ${\mathbf{p}}^{\star }{\mathbf{q}}^{\text{T}}=\alpha (\mathbf{v}\mathbf{A}{\mathbf{q}}^{\text{T}}+\mathbf{v}{\mathbf{w}}^{\text{T}})+\alpha (\mathbf{v}\mathbf{A}{\mathbf{q}}^{\text{T}}+\mathbf{v}{\mathbf{w}}^{\text{T}})r_v$. Now substitute for $r_v$,

$$\begin{array}{cc}\hfill {\mathbf{p}}^{\star }{\mathbf{q}}^{\text{T}}& =\alpha (\mathbf{v}\mathbf{A}{\mathbf{q}}^{\text{T}}+\mathbf{v}{\mathbf{w}}^{\text{T}})+\alpha (\mathbf{l}{\mathbf{q}}^{\text{T}}-\mathbf{v}{\mathbf{w}}^{\text{T}})\hfill \\ \hfill & =\alpha (\mathbf{v}\mathbf{A}{\mathbf{q}}^{\text{T}}+\mathbf{l}{\mathbf{q}}^{\text{T}})\text{.}\hfill \end{array}$$

Multiply equation (2) by $\mathbf{q}$ and substitute $\mathbf{v}\mathbf{A}{\mathbf{q}}^{\text{T}}+\mathbf{l}{\mathbf{q}}^{\text{T}}=\mathbf{v}{\mathbf{q}}^{\text{T}}$. Hence ${\mathbf{p}}^{\star }{\mathbf{q}}^{\text{T}}=\alpha \mathbf{v}{\mathbf{q}}^{\text{T}}$, which establishes (iii).

Hence, production-prices and labour-values, although non-proportional, are nonetheless one-to-one in the aggregate. Profit, despite appearances, is a money representation of surplus-labour.

But the first critic of the transformation is Marx himself. He immediately observes that “the cost-price of a commodity equalled the value of the commodities consumed in its production” (Marx, [1894] 1971, p. 165). Marx’s ‘prices of production’, defined by equation (6), are calculated on the basis of untransformed cost-prices, $\alpha (\mathbf{v}\mathbf{A}+\mathbf{l}(\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}))$, which are proportional to labour-value. But since this assumption is false “there is always the possibility of an error if the cost-price of a commodity in any particular sphere is identified with the [labour-]value of the means of production consumed by it” (Marx, [1894] 1971, p. 165). As Marco Lippi (1979, p. 47) remarks, “the magnitudes on the basis of which surplus-value has been redistributed — that is, capital advanced, measured in [labour-]value — are not identical to the prices at which elements of capital are bought on the market. He therefore admits that the prices previously calculated must be adjusted”. However, Marx does not pursue the adjustment but instead remarks that “our present analysis does not necessitate a closer examination of this point” (Marx, [1894] 1971, p. 165).

Once we make this adjustment then production prices are not defined by Marx’s equation (6) but by equation (3). Now Marx’s three aggregate equalities do not hold, except in certain special cases. The transformation problem is then the general impossibility of satisfying Marx’s conservation conditions. In fact, we can deduce:

Proposition 4. Marx’s three equalities are true only if the economy satisfies the special condition, $\mathbf{v}(\mathbf{I}-(\mathbf{A}+{\overline{\mathbf{w}}}^{\text{T}}\mathbf{l})(1+r)){\mathbf{q}}^{\text{T}}=0$.

Proof. (i) If total profit is proportional to total surplus-labour then

$$\begin{array}{ccc}\hfill (\mathbf{p}\mathbf{A}+\mathbf{l}w){\mathbf{q}}^{\text{T}}r& =\alpha (1-\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}})\mathbf{l}{\mathbf{q}}^{\text{T}}\text{,}\hfill & \hfill \text{(7)}\end{array}$$

where $\alpha$ is the constant of proportionality. (ii) If the profit-rate equals the labour-value profit-rate substitute $r$ from (5) to get

$$\begin{array}{ccc}\hfill (\mathbf{p}\mathbf{A}+\mathbf{l}w){\mathbf{q}}^{\text{T}}& =\alpha (\mathbf{v}\mathbf{A}{\mathbf{q}}^{\text{T}}+\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}\mathbf{l}{\mathbf{q}}^{\text{T}})\text{.}\hfill & \hfill \text{(8)}\end{array}$$

(iii) If the total price of the gross product is proportional to its labour-value then $\mathbf{p}{\mathbf{q}}^{\text{T}}=\alpha \mathbf{v}{\mathbf{q}}^{\text{T}}$. Price equation (3) implies that

$$\begin{array}{ccc}\hfill (\mathbf{p}\mathbf{A}+\mathbf{l}w){\mathbf{q}}^{\text{T}}(1+r)& =\alpha \mathbf{v}{\mathbf{q}}^{\text{T}}\text{.}\hfill & \hfill \text{(9)}\end{array}$$

Substitute (9) into (8) to get $\mathbf{v}{\mathbf{q}}^{\text{T}}=(\mathbf{v}\mathbf{A}{\mathbf{q}}^{\text{T}}+\mathbf{v}{\overline{\mathbf{w}}}^{\text{T}}\mathbf{l}{\mathbf{q}}^{\text{T}})(1+r)$, which can be rearranged into the form

$$\begin{array}{ccc}\hfill \mathbf{v}(\mathbf{I}-(\mathbf{A}+{\overline{\mathbf{w}}}^{\text{T}}\mathbf{l})(1+r)){\mathbf{q}}^{\text{T}}& =0\text{.}\hfill & \hfill \text{(10)}\end{array}$$

Hence Marx’s equalities (i), (ii) and (iii), with a given constant of proportionality $\alpha$, imply (10).

Proposition 4 specifies a macroeconomic constraint between labour-values, income distribution and the scale of production. Conditions that satisfy the constraint are zero profit, a uniform organic composition of capital, or a scale of production in certain special proportions (for further details see Abraham-Frois and Berrebi, 1997, chapter 6). But, in general, there is no economic reason why this macroeconomic constraint should hold, especially as income distribution and the scale of production vary independently of labour-values. In consequence, a conservative transformation does not exist and “there is no rigorous quantitative connection between the labour time accounts arising from embodied labour coefficients and the phenomenal world of money price accounts” (Foley, 2000, p. 17).

The transformation problem is the primary reason for the modern rejection of the logical possibility of a labour theory of value. The debate has generated a large literature spanning over one hundred years. Ian Steedman (1981) provides the definitive statement of the negative consequences for Marx’s value theory. First, the theory is internally inconsistent because Marx “assumes that [$r_v$] is the rate of profit but then derives the result that prices diverge from [labour-]values, which means precisely, in general, that [$r_v$] is not the rate of profit” (Steedman, 1981, p. 31). Second, the theory is redundant because “profits and prices cannot be derived from the ordinary [labour-]value schema, that [$r_v$] is not the rate of profit and that total profit is not equal to surplus value” (Steedman, 1981, p. 48). Steedman notes, following Paul Samuelson (1971), that given a technique and a real wage (the “physical schema”) one can determine (a) profits and prices and (b) labour-values. But, in general, there is “no way” of relating (a) and (b).

Despite Marx’s efforts it appears that a theory of value based exclusively on labour-cost cannot account for price phenomena or the substance of capitalist profit.

4. Total labour costs

Having stated the major problems of the classical labour theory of value we can now turn to understanding why they exist. Clearly, prices and labour-values are incommensurate because a price depends on a profit-rate but a labour-value does not. But we need to dig deeper, and apply conceptual analysis to the concept “labour-value”, to discover the fundamental reason why money costs and labour costs diverge. First, I will examine two related properties of labour-values, which are subtle and normally overlooked, in the context of an economy where capitalist profits are absent.

4.1. The independence of labour-values from the real wage

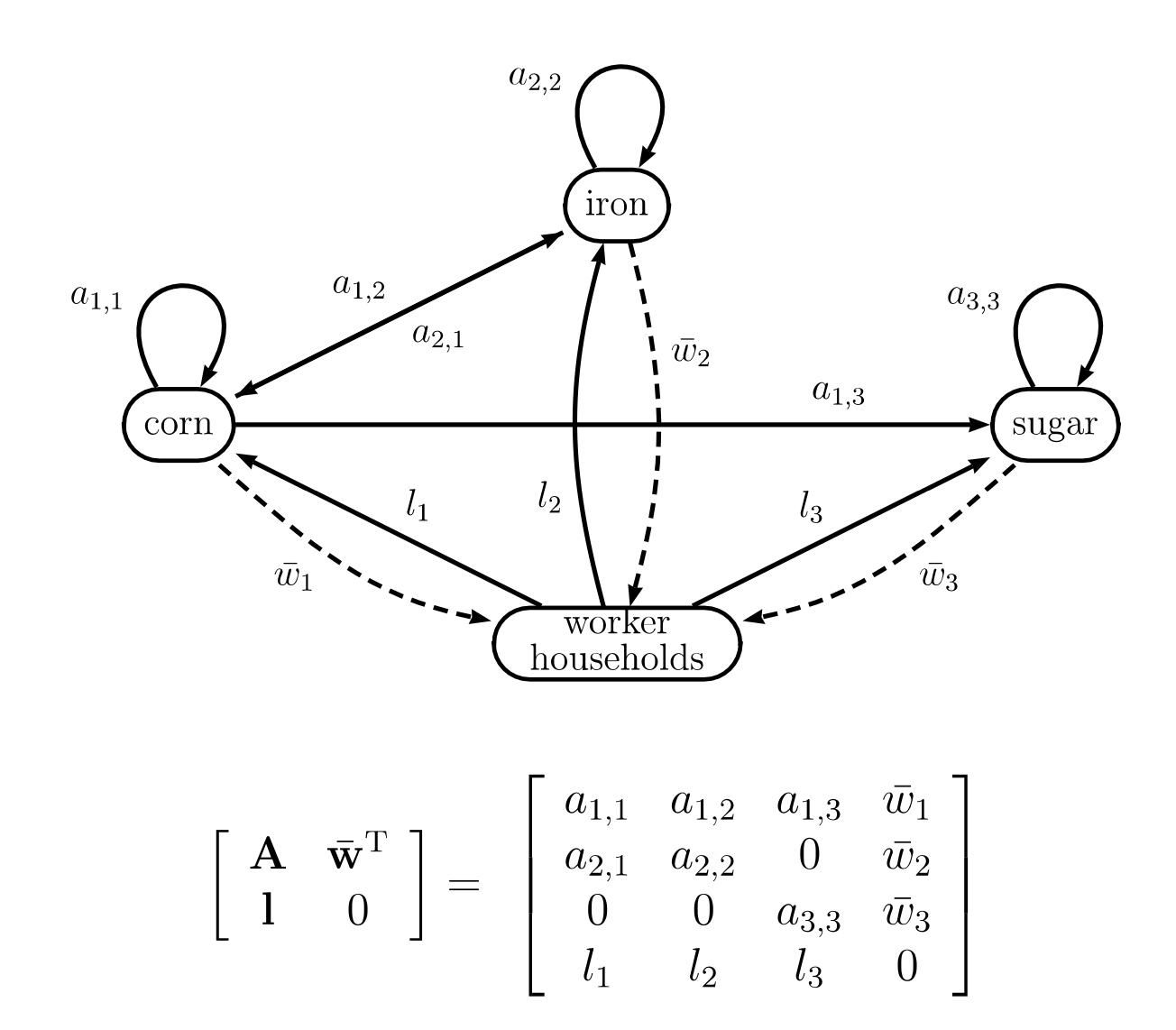
Figure 2. A social accounting matrix for an example 3-sector simple production economy depicted as a directed graph. This graph is identical to figure 1 apart from the addition of worker consumption $\overline{\mathbf{w}}$.

Figure 2 depicts an example economy where all household income takes the form of wages (cf. Marx’s concept of “simple production”). There is no government or financial sector. The social accounting matrix therefore simply specifies the technique and the real wage consumed per unit of labour supplied, $\overline{\mathbf{w}}$.

Earlier, I described the computation of a labour-value as a procedure of vertical integration. If we perform this procedure in the context of a social accounting matrix we immediately notice that some input paths are ignored. Specifically, the real wage inputs to worker households, drawn as dashed arcs in figure 2, are not vertically integrated. So the labour supplied to produce the real wage, which maintains and reproduces the working class, is excluded as a component of the labour cost of producing commodities. Why is this coexisting labour not counted?

A labour-value is the answer to the question, “What is the total coexisting labour supplied to reproduce 1 unit of a commodity?” But it is not the answer to the question, “What is the total coexisting labour supplied to reproduce 1 unit of a commodity and reproduce the labour that reproduced that unit?” Measuring the cost of reproducing the very resource that serves as the measure of cost would be like measuring the height of a tree with a metre rod and including the length of the rod as part of the tree’s height.

We can look at this another way. Any system of measurement defines a standard unit (e.g., the metre). We do not ask, “How many metres are in one metre?” since the measure of the standard unit is by definition a unit of the standard. In a labour theory of value the question, “What is the labour-value of one unit of direct labour?” is similarly ill-formed: the real cost of 1 hour of labour, measured by labour time, is 1 hour. No further reduction is possible or required. The self-identity of the measuring standard is a conceptual necessity in any system of measurement. So whether workers consume one bushel or a thousand bushels of corn to supply a unit of direct labour makes no difference to the labour-value of that unit of direct labour: an hour of labour-time is an hour of labour-time. In consequence, the procedure of vertical integration, when applied to a social accounting matrix, always terminates at labour inputs and does not further reduce labour inputs to the real wage.

For example, Marx notes that the expression ‘labour-value of labour-power’, where labour-power is the capacity to supply labour, denotes the “difficulty of production” of the real wage, which is the conventional level of consumption that reproduces the working class. In contrast, the expression ‘labour-value of labour’ is an oxymoron: “the value of labour is only an irrational expression for the value of labour-power”. The expression, taken literally, is analogous to querying the colour of a logarithm (Marx, [1894] 1971) or the time on the sun (Pollock, 2004). “Labour is the substance, and the immanent measure of value, but has itself no value” (Marx, [1867] 1954, p. 503). In summary, labour-values, as a conceptual necessity, are independent of the scale and composition of the real income of workers.

4.2. Labour-values as total labour costs

Labour-values, then, exclude the reproduction costs of labour (i.e., the coexisting labour supplied to reproduce the real wage). In the context of a “simple production” economy the procedure of vertical integration therefore reduces all real costs (such as corn, iron and sugar) to quantities of direct labour except the cost of labour. Hence classical labour-values, in this context, are “total labour costs”:

Definition 2. The “total labour cost” of a commodity is (i) a measure of the coexisting labour supplied to reproduce it that (ii) only excludes the reproduction cost of labour.

The classical proposition that equilibrium prices of reproducible goods are proportional to labour-values in an “early and rude state” (Smith, [1776] 1994) is not controversial. Indeed, even critics of a labour theory of value accept this (e.g., Samuelson, 1971; Steedman, 1981; Roemer, 1982). Natural prices are proportional to labour-values, that is $\mathbf{p}=w\mathbf{v}$ (see Proposition 1), because both accounting systems, that is money and labour costs, apply the same accounting convention: all commodities are reduced to a scalar measure of total cost — either total money or total labour cost. The accounting systems are dual or mutually consistent and therefore related by the price of labour, $w$.

Consequently, in a “simple production” economy the natural price of a commodity is the wage bill of the total coexisting labour supplied to produce it. Commodities that require more of society’s labour-time to produce sell at higher prices in equilibrium.

Now let us introduce capitalist profit income and determine exactly why this simple relationship breaks down. We shall see that classical labour-values, in the context of capitalist production, no longer satisfy the definition of total labour costs.

5. Capitalist households

The natural prices of an economy with capitalist profit are production prices given by equation 3 where the profit-rate is uniform across all sectors. In this situation capitalists supply money-capital to firms to meet production costs and receive profit income proportional to their advance. This profit mark-up, or price of money-capital, $r$, forms a cost component of the production price.

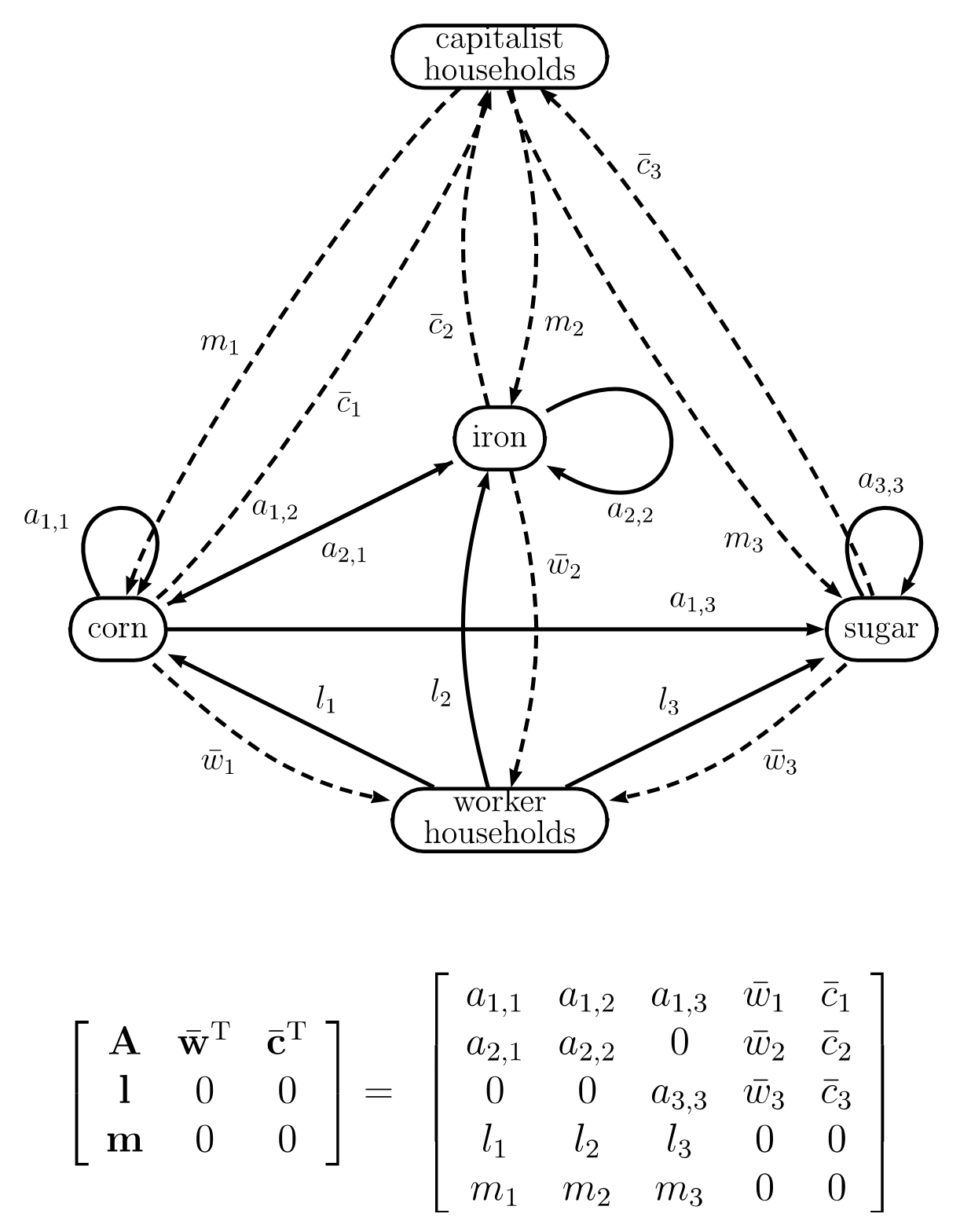
Figure 3. A social accounting matrix for an example 3-sector capitalist economy depicted as a directed graph. This graph is identical to figure 2 apart from the addition of a capitalist household sector.

Figure 3 depicts a social accounting matrix for a capitalist economy where capitalists spend all their profit income on personal consumption and therefore no capital accumulation takes place (cf. Marx’s concept of simple reproduction — Marx, [1867] 1954, chapter 23). ^[14] Simple reproduction is identical to our previous case of simple production apart from the addition of a capitalist household sector that funds the period of production by supplying money-capital to firms in each sector. The firms use the loan capital to purchase input goods and pay wages. The loan is repaid, with interest, at the close of the production period. ^[15] Capitalists purchase consumption goods with their interest income and workers purchase the real wage with their wage income. The social accounting matrix therefore also specifies the distribution of the net product in the form of the real wage and capitalist consumption.

Assume firms do not self-finance. Then the vector of cost prices, or money-capital requirement coefficients, $\mathbf{m}=[m_i]$, where $m_i=\mathbf{p}{\mathbf{A}}^{(i)}+l_{i}w$, denotes the quantity of money-capital supplied to produce unit outputs (see figure 3 and Vickers 1987). A “quantity of money-capital” denotes a sum of loaned money (i.e., an outstanding principal) and the “supply of money-capital” denotes the supply of loan services, which includes loan management and actual transfers of money (at the opening of the production period). The total supply of money-capital is a function of the money-capital requirement coefficients and the scale of production, i.e. $\mathbf{m}{\mathbf{q}}^{\text{T}}$. Note that the quantity of loaned money is not identical to the total stock of money in circulation since “the same mass of actual money can … represent very different masses of money-capital” (Marx, [1894] 1971, p. 510). In other words, a given stock of money may service multiple loans.

Capitalist households receive a bundle of consumption goods $\mathbf{c}$. Figure 3 therefore also specifies capitalist consumption coefficients, $\overline{\mathbf{c}}=(1/\mathbf{m}{\mathbf{q}}^{\text{T}})\mathbf{c}$, which denote consumption per unit of money-capital supplied. ^[16] For example, $\overline{\mathbf{c}}=[10,5]$ indicates that capitalists consume 10 bushels of corn and 5 kilos of sugar per £1 of money-capital supplied to production, where £1 is the unit of account. These coefficients are analogous to worker consumption coefficients, $\overline{\mathbf{w}}=(1/\mathbf{l}{\mathbf{q}}^{\text{T}})\mathbf{w}$, which denote worker consumption per unit of labour supplied. The economy’s net product is then $\mathbf{n}=\mathbf{w}+\mathbf{c}$.

Assume, for simplicity, that the supply of money-capital does not incur direct labour costs, such as the labour of managing and servicing loans. So money-capital is not produced, like a unit of corn, but merely advanced. (Including the direct labour cost of the supply of money-capital would add a new kind of labour activity to our model, and corresponding wage income, but would not remove the fundamental difference between profit and wages: profit is received in virtue of the ownership of capital, whereas the wage is received in virtue of labour supplied.)

6. The divergence of technical and total labour costs

Now that we’ve specified a social accounting matrix for an economy with capitalist profit we can reconsider the process of vertical integration.

Production now additionally requires the supply of money-capital $m_i$ (as shown by the dashed input edges from capitalist households to the system of production in Figure 3). Although the supply of money-capital, in this model, does not incur direct labour costs it does incur indirect labour costs. Capitalists do not advance money-capital for free, either nominally or in real terms. In parallel with the production of unit $i$, and the supply of money-capital $m_i$, capitalists consume commodity bundle $m_i\overline{\mathbf{c}}$. So, a quantity of coexisting labour, $m_i\mathbf{l}{\overline{\mathbf{c}}}^{\text{T}}$, is indeed used-up during the supply of money-capital, specifically the coexisting labour that replaces the goods that capitalists consume.

The classical formula for labour-values (2) ignores this coexisting labour because the supply of money-capital to production is not part of the technique, and therefore is not included in the process of vertical integration (i.e., none of the dashed input arcs from capitalist households in Figure 3 are vertically integrated). Money-capital inputs are treated as an irreducible terminus. In consequence, classical labour-values do not count the labour supplied to replace capitalist consumption goods as part of the ex ante real costs of production.

Of course, we may measure the classical labour-value of any bundle of goods, including capitalist consumption goods. The point to notice, however, is that the classical measure ignores some actual labour supplied during the production of these goods.

Should this ‘missing’ labour be counted as a cost?

The classical authors exclude this labour as a real cost of production without fully recognizing the existence of a theoretical choice. They do not consider the possibility of alternative measures of labour cost. ^[17] However, the labour supplied to produce capitalist consumption goods is not a cost of reproducing labour and therefore necessarily excluded, as a conceptual necessity, from any definition of labour-value (as explained in section 4).

The answer depends, quite simply, on what we want to measure. And what we want to measure depends on the theoretical questions we pose and seek to answer.

For example, classical labour-values, as purely technical measures of labour costs, can answer questions about the productivity of labour over time independent of the distribution of income (see especially Flaschel, 2010, pt. 1). The reciprocal of a classical labour-value measures the quantity of the commodity produced by a unit of coexisting labour, independent of the wider institutional context in which this activity occurs

But if we want to measure total labour costs, that is measure the actual labour supplied to reproduce commodities in the complete circumstances in which production takes place, then we cannot use classical labour-values. By definition total labour costs reduce all real costs to labour, except the cost of producing the real wage. But classical labour-values exclude the additional labour cost of producing capitalist consumption goods; hence, they do not measure total labour costs. This conclusion is merely a consequence of definitions.

Money-capital, in the circumstances of capitalist production, is not a technical input to production but nonetheless is an actual material prerequisite to production. Marx (1974, Ch. 18, pt. 2) describes money-capital as the “primus motor of every incipient business, and as its continual motor.” And, in capitalist conditions, a commodity cannot be produced without capitalists supplying money-capital and workers simultaneously performing tributary or “surplus” labour to replace the commodities that capitalists consume. Classical labour-values, as a purely technical measure of labour cost, exclude this tributary labour as a real cost of production. A measure of total labour costs, by definition, must include it. Let us now do that.

7. Total labour costs: super-integrated labour values

Recall that coefficient ${\overline{c}}_i$ denotes the quantity of commodity $i$ consumed by capitalists households per unit of money-capital supplied (e.g., 1 pound of sugar per £1 of money-capital supplied). And $m_j$ is the money-capital supplied by capitalists to sector $j$ per unit output of commodity $j$ (e.g., £10 of money-capital per 1 tonne of iron). Note that the product, ${\overline{c}}_i{m}_j$ is therefore the quantity of commodity $i$ consumed by capitalist households per unit output of commodity $j$ (e.g., 10 pounds of sugar consumed per tonne of iron produced).

The social accounting matrix, in figure 3, therefore implicitly defines the $n\times n$ matrix of capitalist consumption coefficients,

$$\mathbf{C}={\overline{\mathbf{c}}}^{\text{T}}\mathbf{m}=[c_{i,j}]\text{,}$$

where each $c_{i,j}={\overline{c}}_i{m}_j$ is the quantity of commodity $i$ consumed by capitalist households per unit output of commodity $j$. Matrix $\mathbf{C}$, in consequence, is a “capitalist consumption matrix” that specifies how the production of new commodities is synchronised with the consumption of existing commodities by capitalist households. Matrix $\mathbf{C}$ encapsulates the real costs of supplying money-capital to the different sectors of the economy. Note that matrix $\mathbf{C}$ is a physical input-output matrix that specifies relative material flows of commodities; for example, each element $c_{i,j}$ of $\mathbf{C}$ is measured in units identical to the corresponding element $a_{i,j}$ of the technique $\mathbf{A}$. We can therefore define the technique augmented by capitalist consumption as

$$\tilde{\mathbf{A}}=\mathbf{A}+\mathbf{C}=[{\tilde{a}}_{i,j}]\text{,}$$

where each ${\tilde{a}}_{i,j}=a_{i,j}+c_{i,j}$ is the quantity of commodity $i$, including that consumed by capitalists, directly used-up per unit output of $j$.

We can now compute the total labour costs for this capitalist economy by vertically integrating over the technique augmented by capitalist consumption: Production of commodity $i$ uses-up direct labour $l_i$ and the bundle of input commodities ${\mathbf{A}}^{(i)}+m_i{\overline{\mathbf{c}}}^{\text{T}}=$ ${\mathbf{A}}^{(i)}+{\mathbf{C}}^{(i)}$, consisting of means of production and capitalist consumption goods. This bundle is replaced by the simultaneous expenditure of labour $\mathbf{l}({\mathbf{A}}^{(i)}+{\mathbf{C}}^{(i)})$ operating in parallel, which itself uses-up input bundle $\tilde{\mathbf{A}}({\mathbf{A}}^{(i)}+{\mathbf{C}}^{(i)})$. To count all the coexisting labour we continue the sum; that is,

$$\begin{array}{cc}\hfill {\tilde{v}}_i=l_i& +\mathbf{l}({\mathbf{A}}^{(i)}+{\mathbf{C}}^{(i)})+\mathbf{l}\tilde{\mathbf{A}}({\mathbf{A}}^{(i)}+{\mathbf{C}}^{(i)})\hfill \\ \hfill & +\mathbf{l}{\tilde{\mathbf{A}}}^2({\mathbf{A}}^{(i)}+{\mathbf{C}}^{(i)})+\dots \hfill \\ \hfill =l_i& +\mathbf{l}(\mathbf{I}+\tilde{\mathbf{A}}+{\tilde{\mathbf{A}}}^2+\dots )({\mathbf{A}}^{(i)}+{\mathbf{C}}^{(i)})\hfill \\ \hfill =l_i& +\mathbf{l}({\sum }_{n=0}^{\infty }{\tilde{\mathbf{A}}}^n)({\mathbf{A}}^{(i)}+{\mathbf{C}}^{(i)})\text{.}\hfill \end{array}$$

The vector $\tilde{\mathbf{v}}$ of total coexisting labour supplied to reproduce a unit bundle $\mathbf{u}=[1]$ of commodities is

$$\tilde{\mathbf{v}}=\mathbf{l}+\mathbf{l}({\sum }_{n=0}^{\infty }{\tilde{\mathbf{A}}}^n)(\mathbf{A}+\mathbf{C})=\mathbf{l}{\sum }_{n=0}^{\infty }{\tilde{\mathbf{A}}}^n\text{.}$$

Rewrite the infinite series, such that $\tilde{\mathbf{v}}=\mathbf{l}(\mathbf{I}-\tilde{\mathbf{A}}{)}^{-1}$; and therefore:

Definition 3. “Super-integrated labour-values”, $\tilde{\mathbf{v}}$, are

$$\begin{array}{ccc}\hfill \tilde{\mathbf{v}}& =\tilde{\mathbf{v}}\tilde{\mathbf{A}}+\mathbf{l}\text{,}\hfill & \hfill \text{(11)}\end{array}$$

where $\tilde{\mathbf{A}}=\mathbf{A}+\mathbf{C}$ is the technique augmented by capitalist consumption.

A super-integrated labour-value is a new measure of labour cost constructed by vertically integrating both the technique and the real cost of capitalist consumption, which satisfies the definition of a total labour cost in the context of simple reproduction.

Let us draw some contrasts between classical and super-integrated labour-values. The classical formula, $\mathbf{v}=\mathbf{v}\mathbf{A}+\mathbf{l}$, is a property of the technique and measures technical labour costs. In contrast, the super-integrated formula, $\tilde{\mathbf{v}}=\tilde{\mathbf{v}}\tilde{\mathbf{A}}+\mathbf{l}$, is a property of the social accounting matrix ^[18], including the distribution of real income, and measures total labour costs.

Classical labour-values are the sum of direct labour, $\mathbf{l}$, plus indirect labour, $\mathbf{v}\mathbf{A}$. Super-integrated labour-values are the sum of direct labour, $\mathbf{l}$, and indirect labour, $\tilde{\mathbf{v}}\mathbf{A}$, plus the ‘super-indirect’ labour, $\tilde{\mathbf{v}}\mathbf{C}$, which is tributary labour devoted to the production of capitalist consumption goods. In general, $\tilde{\mathbf{v}}>\mathbf{v}$. But in the absence of “profits on stock” the super-integrated labour-values reduce to classical labour-values.

Classical labour-values count all household consumption (whether workers or capitalists) as net output and therefore not a cost of production; in contrast, superintegrated labour-values count capitalist consumption as a real cost of production. Both schemes, of course, assign an ex post labour-value to the real income of capitalists, since this bundle of goods requires labour resources to produce it. However, in the classical scheme, the direct labour supplied to produce capitalist consumption is “surplus labour”, i.e. supplied “gratis”, and therefore, by definition, does not constitute an ex ante cost of production (e.g., see Marx, [1867] 1954, chapter 18; Marx, [1894] 1971, part V, chapter 32).

The definition of super-integrated labour-values does not provide or rely upon any theory of income distribution or profit and is independent of the possible reasons why workers and capitalists consume specific consumption bundles. However, in order to calculate super-integrated labour-values the distribution of real income must be given, in much the same manner that, in order to calculate production prices, the distribution of nominal income must be given.

Both classical and super-integrated labour-values are functions of real or ‘physical’ data alone, which we can operationalise without reference to monetary phenomena, and constitute entirely self-consistent labour-cost accounting schemes. ^[19] They measure different aspects of the same economy by applying different cost-accounting conventions to the analysis of the labour process. As we shall see, we need both measures to answer the full range of questions posed by a labour theory of value.

8. The category-mistake: conflating technical and total labour costs

Now that we’ve distinguished between technical and total labour costs we can understand the fundamental reason why money and labour costs diverge.

Money-capital has a price, the profit-rate, which is a ‘mark up’ component of the money cost of a commodity. Money-capital also has a real cost, which, in the case of simple reproduction, is capitalist consumption. Production prices, as total money costs, include the profit-rate as a money cost of production, and therefore prices depend on the distribution of nominal income. But classical labour-values, as technical labour costs, exclude the labour cost of money-capital as a real cost of production, and therefore labour-values are independent of the distribution of real income. In summary, the dual accounting systems apply different cost conventions and, in consequence, there cannot be a one-to-one relationship between prices and labour-values: in the classical framework the profit-rate component of money costs refers to labour costs that are not counted.

The asymmetrical treatment of the commodity money-capital — present as a money cost in the price system but absent as a real cost in the labour-value system — is the fundamental reason for the divergence of money and labour costs. A quantitative mismatch necessarily arises if total money costs are compared to partial labour costs.

The classical contradictions of the labour theory of value are the manifestation of the category-mistake of supposing that technical costs are of the same logical type as total costs. Hence Ricardo’s search for an invariable measure and Marx’s transformation are theoretical attempts to find Ryle’s “elusive and insubstantial man” or “ghost”.

The classical category-mistake has been, and continues to be, the major obstacle toward a deeper understanding of the relationship between social labour and monetary phenomena. For example, it has directed theoretical attention toward the contradictions and away from the existence of a simple one-to-one quantitative relation between production prices and labour costs.

Definition 4. A “steady-state economy” produces quantities, $\mathbf{q}=\mathbf{q}{\mathbf{A}}^{\text{T}}+\mathbf{w}+\mathbf{c}$, at prices, $\mathbf{p}=(\mathbf{p}\mathbf{A}+\mathbf{l}w)(1+r)$, where workers and capitalists spend what they earn, $\mathbf{p}{\mathbf{w}}^{\text{T}}=\mathbf{l}{\mathbf{q}}^{\text{T}}w$ and $\mathbf{p}{\mathbf{c}}^{\text{T}}=(\mathbf{p}\mathbf{A}+\mathbf{l}w){\mathbf{q}}^{\text{T}}r$.

Theorem 1. The production-prices of a steady-state economy are proportional to super-integrated labour-values, $\mathbf{p}=\tilde{\mathbf{v}}w$.

Proof. In a steady-state economy, $\mathbf{p}{\mathbf{c}}^{\text{T}}=(\mathbf{p}\mathbf{A}{\mathbf{q}}^{\text{T}}+\mathbf{l}{\mathbf{q}}^{\text{T}}w)r$. Recall that cost prices $\mathbf{m}=\mathbf{p}\mathbf{A}+\mathbf{l}w$. Hence $r=\mathbf{p}{\mathbf{c}}^{\text{T}}/\mathbf{m}{\mathbf{q}}^{\text{T}}=\mathbf{p}{\overline{\mathbf{c}}}^{\text{T}}$. Substitute $r=\mathbf{p}{\overline{\mathbf{c}}}^{\text{T}}$ into price equation (3) to get

$$\begin{array}{cc}\hfill \mathbf{p}& =(\mathbf{p}\mathbf{A}+\mathbf{l}w)+(\mathbf{p}\mathbf{A}+\mathbf{l}w)\mathbf{p}{\overline{\mathbf{c}}}^{\text{T}}\hfill \\ \hfill & =(\mathbf{p}\mathbf{A}+\mathbf{l}w)+\mathbf{m}\mathbf{p}{\overline{\mathbf{c}}}^{\text{T}}\hfill \\ \hfill & =\mathbf{p}\mathbf{A}+\mathbf{p}{\overline{\mathbf{c}}}^{\text{T}}\mathbf{m}+\mathbf{l}w\hfill \\ \hfill & =\mathbf{p}(\mathbf{A}+{\overline{\mathbf{c}}}^{\text{T}}\mathbf{m})+\mathbf{l}w\hfill \\ \hfill & =\mathbf{p}\tilde{\mathbf{A}}+\mathbf{l}w\text{.}\hfill \end{array}$$

Hence $\mathbf{p}=\mathbf{l}(\mathbf{I}-\tilde{\mathbf{A}}{)}^{-1}w=\tilde{\mathbf{v}}w$, by equation (11).

In consequence, in a steady-state economy, the production-price of a commodity is the wage bill of the total coexisting labour supplied to reproduce it. Commodities that require more labour time to produce sell at proportionally higher prices in equilibrium. Natural prices — whether in an “early and rude state” or in our late and civilised times — vary one-to-one with total labour costs. ^[20]

How general is this proposition? The definition of total labour cost applies to any social accounting matrix. Hence, in more complex models, total labour costs include additional real costs of production, over and above capitalist consumption. For example, in Chapter 5 we shall see that total labour-values, in circumstances of expanded reproduction with proportionate or non-proportionate growth, are “vertically super-integrated labour coefficients” that additionally include the labour cost of supplying the net investment goods required to expand the scale of production. The natural prices of growing economies are therefore also proportional to total labour costs.

Many possible generalisations remain unexplored, however. For example, the robustness of such equivalence theorems have yet to be tested in the context of (i) more complex social accounting matrices, which include capitalist savings, a public sector, credit money etc., (ii) production with fixed capital, and (iii) systems of joint production. In Chapter 7 I investigate a nonlinear dynamic model of classical macrodynamics where market prices gravitate to natural prices proportional to the super-integrated labour-values.

Now we’ve identified the category-mistake, and introduced a distinction between classical and total labour costs, we can finally return to the classical problems.

9. Dissolution of the problem of an invariable measure of value

Ricardo conflates two concepts of “difficulty of production” that we can now distinguish.

Classical labour-values, $\mathbf{v}$, measure “difficulty of production” independent of an economy’s institutional structure and distributive rules. A classical labour-value, $v_i$, is therefore a counterfactual measure of the total coexisting labour that would be supplied to reproduce commodity-type $i$ if workers did not perform tributary labour during the production of commodities.

Super-integrated labour-values, $\tilde{\mathbf{v}}$, measure “difficulty of production” dependent on an economy’s institutional structure and distributive rules. A super-integrated labour-value, ${\tilde{v}}_i$, is therefore an actual measure of the total coexisting labour supplied to reproduce commodity-type $i$ given that workers perform additional tributary labour during the production of commodities.

Ricardo wished to reduce the structure of natural prices (relative value) to “difficulty of production” (absolute value) measured in terms of some real cost basis, such as labour costs. Classical labour-values are an invariable measure of absolute value independent of the distribution of income and therefore we can use them to say, without “embarrassment” or equivocation, that “commodity A is now less valuable than one year ago” in the strictly technical sense that commodity A requires less labour resources to reproduce than it once did. But it is a category-mistake to hope or expect, as Ricardo did, that this standard can also explain the structure of natural prices.

Super-integrated labour-values, in contrast, explain the structure of natural prices in terms of objective quantities of coexisting labour supplied to produce commodities (Theorem 1). Hence they provide that all-important one-to-one relation, required by a labour theory of value, between absolute values, measured in terms of labour time, and relative prices.

The point is this: classical labour-values answer distribution-independent questions about the technical “difficulty of production” of commodities, whereas super-integrated labour-values answer distribution-dependent questions about the actual “difficulty of production” of commodities. In consequence — and on condition we apply the appropriate concept of “difficulty of production” in each case — we can justifiably make public statements about changes in objective value, independent of the distribution of income and simultaneously claim that relative values covary with absolute values, and thereby explain the structure of natural prices in terms of labour costs. Ricardo’s belief in another “less powerful cause” of the variation of relative values, which is unrelated to labour costs, is caused by the category-mistake. Ricardo’s problem therefore dissolves.

10. Dissolution of the transformation problem

Marx employs classical labour-values to address issues in the theory of exploitation (e.g., how many hours do workers supply in excess of the time required to produce their real wage?) and, in addition, issues in the theory of economic value (e.g., what does the nominal unit of account, such as £1, “express” or measure? what is the “substance” of profit? etc.) The distinction between classical and total labour-values permits us to separate these concerns and therefore avoid the transformation problem while preserving Marx’s analysis of the capitalist labour process.

Let $\mathbf{n}=\mathbf{w}+\mathbf{c}$ be the net product of the economy, where $\mathbf{c}$ is the consumption bundle of capitalists. The total working day equals the classical labour-value of the net product, $\mathbf{l}{\mathbf{q}}^{\text{T}}=\mathbf{v}{\mathbf{n}}^{\text{T}}$:

Proposition 5. The total labour supplied equals the classical labour-value of the net product, $\mathbf{l}{\mathbf{q}}^{\text{T}}=\mathbf{v}{\mathbf{n}}^{\text{T}}$.

Proof. Since $\mathbf{q}=\mathbf{q}{\mathbf{A}}^{\text{T}}+{\mathbf{n}}^{\text{T}}$ it follows that

$$\begin{array}{cc}\hfill \mathbf{v}(\mathbf{I}-\mathbf{A}){\mathbf{q}}^{\text{T}}=\mathbf{v}{\mathbf{n}}^{\text{T}}\text{.}& \text{(12)}\hfill \end{array}$$

But $\mathbf{v}=\mathbf{l}(\mathbf{I}-\mathbf{A}{)}^{-1}$. Replace $\mathbf{v}$ on the LHS of (12) to get $\mathbf{l}{\mathbf{q}}^{\text{T}}=\mathbf{v}{\mathbf{n}}^{\text{T}}$.

Marx splits the working day into necessary labour, $\mathbf{v}{\mathbf{w}}^{\text{T}}$, which is the part ‘technically necessary’ to reproduce workers, and surplus labour, $\mathbf{v}{\mathbf{n}}^{\text{T}}-\mathbf{v}{\mathbf{w}}^{\text{T}}$ ($=\mathbf{v}{\mathbf{c}}^{\text{T}}$), which is an additional part appropriated by capitalists. Marx’s normative point, among other things, is that production could occur without the performance of this surplus labour, and yet workers could continue to consume the same real wage.

Super-integrated labour-values, by definition, include surplus labour as a cost of production. In consequence, they do not split the working day into necessary and surplus parts. In terms of total labour costs the whole working day, $\mathbf{l}{\mathbf{q}}^{\text{T}}=\tilde{\mathbf{v}}{\mathbf{w}}^{\text{T}}$, is ‘socially necessary’ to reproduce workers given that the real wage cannot be produced without the simultaneous performance of surplus labour for capitalists:

Proposition 6. The total labour supplied equals the super-integrated labour-value of the real wage, $\mathbf{l}{\mathbf{q}}^{\text{T}}=\tilde{\mathbf{v}}{\mathbf{w}}^{\text{T}}$.

Proof. In a steady-state economy, $\mathbf{l}{\mathbf{q}}^{\text{T}}w=\mathbf{p}{\mathbf{w}}^{\text{T}}$. Use Theorem 1 to substitute for $\mathbf{p}$ and the conclusion follows.

We can therefore restate Marx’s concept of “surplus labour” in terms of super-integrated and classical labour-values. Surplus labour is the difference between (i) the labour time socially necessary and (ii) the labour time technically necessary to reproduce workers, i.e. $\tilde{\mathbf{v}}{\mathbf{w}}^{\text{T}}-\mathbf{v}{\mathbf{w}}^{\text{T}}$ (since $\tilde{\mathbf{v}}{\mathbf{w}}^{\text{T}}=\mathbf{l}{\mathbf{q}}^{\text{T}}=\mathbf{v}{\mathbf{n}}^{\text{T}}$).

Splitting the working day this way is both logical and illuminating, regardless of any relationship it may have to the price system, since it provides the quantitative basis for a normative critique of capitalist production. But it is a category-mistake to hope or expect, as Marx did, that a technical, and therefore partial, measure of surplus labour has a one-to-one relation with a total measure of money profit. Money profit, in fact, has a one-to-one relation with total surplus labour, $\tilde{\mathbf{v}}{\mathbf{n}}^{\text{T}}-\tilde{\mathbf{v}}{\mathbf{w}}^{\text{T}}$, not Marx’s surplus labour, $\mathbf{v}{\mathbf{n}}^{\text{T}}-\mathbf{v}{\mathbf{w}}^{\text{T}}$:

Proposition 7. Money profit, $(\mathbf{p}\mathbf{A}+\mathbf{l}w){\mathbf{q}}^{\text{T}}r$, is proportional to total surplus labour, $\tilde{\mathbf{v}}{\mathbf{n}}^{\text{T}}-\tilde{\mathbf{v}}{\mathbf{w}}^{\text{T}}$.

Proof. In a steady-state economy, $\mathbf{p}{\mathbf{c}}^{\text{T}}=(\mathbf{p}\mathbf{A}+\mathbf{l}w){\mathbf{q}}^{\text{T}}r$. Hence we need to demonstrate $\mathbf{p}{\mathbf{c}}^{\text{T}}\propto \tilde{\mathbf{v}}{\mathbf{n}}^{\text{T}}-\tilde{\mathbf{v}}{\mathbf{w}}^{\text{T}}$. Theorem 1 implies $\mathbf{p}{\mathbf{c}}^{\text{T}}=\tilde{\mathbf{v}}{\mathbf{c}}^{\text{T}}w$. And $\tilde{\mathbf{v}}{\mathbf{c}}^{\text{T}}w=(\tilde{\mathbf{v}}{\mathbf{n}}^{\text{T}}-\tilde{\mathbf{v}}{\mathbf{w}}^{\text{T}})w$ by the definition of $\mathbf{n}$.

In the context of the transformation problem, the Marxist tradition in general has accepted divergence of production prices from labour-values but defended conservation of labour-value in price, whereas critics have also accepted divergence but denied conservation of labour-value in price. But both sides of the argument are mistaken: once we measure in terms of total labour costs there is no divergence and there is aggregate conservation. Production prices represent total labour costs, i.e. super-integrated labour-values, and therefore capitalist profit is a money representation of labour time.

Corollary 1. All Marx’s equalities obtain when labour-values measure total labour costs, specifically (i) the profit-rate equals the labour-value profit-rate, (ii) total profit is proportional to surplus labour, and (iii) total production price is proportional to total labour-value.

Proof. This is a trivial consequence of Theorem 1, i.e. the proportionality of production prices and total labour costs.

In consequence, the standard criticisms of the classical labour theory of value do not apply: super-integrated labour-values are not internally inconsistent, since the money profit-rate equals the labour-value profit-rate, nor redundant, since production prices can be derived from labour-values by scaling by the money wage $w$. Hence a theory of value based exclusively on labour cost can account for price phenomena: total labour costs and prices are “two sides of the same coin”. The transformation problem therefore dissolves.

This conclusion, it should be emphasised, undermines the basis for the claim that a labour theory of value must be logically incoherent because prices and classical labour-values are quantitatively incommensurable in linear production models (e.g., Samuelson, 1971; Lippi, 1979; Steedman, 1981).

Conclusion

The classical labour theory of value commits the category-mistake of supposing that classical labour-values, which measure strictly technical or material costs of production, are of the same logical type as natural prices, which measure non-technical or social costs of production, and therefore labour-values and prices, under appropriate equilibrium conditions, are mutually consistent. This category-mistake is the cause of Ricardo’s problem of an invariable measure of value and Marx’s transformation problem.

This essay has drawn a new distinction, lacking in the classical theory, between a “technical” and a “total” measure of labour cost, where a total labour cost includes additional real costs incurred in virtue of non-technical conditions of production, such as production financed by money-capital. Classical labour-values, in this more refined conceptual framework, apply to distribution-independent questions about an economy, such as the productivity of labour or measuring the surplus-labour supplied by workers; whereas total labour-values apply to distribution-dependent questions, such as the relationship between nominal prices and the actual labour time required to produce commodities (i.e., issues in the theory of economic value). The classical problems dissolve by generalising the classical labour theory to apply both concepts in the appropriate contexts.

The category-mistake has misdirected theoretical attention toward the contradictions and away from the fact that a commodity’s natural price is the wage bill of the total coexisting labour supplied to produce it (Theorem 1). By ridding ourselves of longstanding conceptual confusions we discover the logical possibility of a new theoretical object: a more general labour theory of value with an invariable measure of value and without a transformation problem. ^[21]

References

• Abraham-Frois, G., Berrebi, E., 1997. Prices, Profits and Rhythms of Accumulation. Cambridge University Press, Cambridge
• Dmitriev, V. K., 1974. Economic essays on value, competition and utility. Cambridge University Press, London, originally published between 1898-1902, Moscow.
• Elson, D., 1979. “The value theory of labour.” In: Elson, D. (Ed.), Value: The Representation of Labour in Capitalism. CSE Books, London.
• Fine, B., Saad-Filho, A., 2004. Marx’s Capital, 4th Edition. Pluto Press, London.
• Flaschel, P., 2010. Topics in Classical Micro- and Macroeconomics: Elements of a Critique of Neoricardian Theory. Springer, New York.
• Foley, D. K., 2000. “Recent developments in the labour theory of value.” Review of Radical Political Economics 32 (1), 1-39.
• Hodgskin, I., 1825. Labour defended against the claims of capital: or, The unproductiveness of capital proved with reference to the present combinations amongst journeymen. B. Steil, London.
• Howard, M. C., King, J. E., 1989. A History of Marxian Economics, Volume I, 18831929. Macmillan, London.
• Howard, M. C., King, J. E., 1992. A History of Marxian Economics, Volume II, 19291990. Macmillan, London.
• Kurz, H. D., Salvadori, N., 1995. Theory of Production — a Long Period Analysis. Cambridge University Press, Cambridge.
• Laibman, D., 2002. Value and the quest for the core of capitalism. Review of Radical Political Economics 34, 159-178.
• Lancaster, K., 1968. Mathematical economics. Dover Publications, New York.
• Lippi, M., 1979. Value and Naturalism. New Left Books, London.
• Marx, K., 1974. Capital. Vol. 2. Progress Publishers, Moscow.
• Marx, K., 2000. Theories of Surplus Value. Prometheus Books, New York.
• Marx, K., [1867] 1954. Capital. Vol. 1. Progress Publishers, Moscow.
• Marx, K., [1894] 1971. Capital. Vol. 3. Progress Publishers, Moscow.
• Nuti, D. M., 1974. Introduction. In: Nuti, D. M. (Ed.), V. K. Dmitriev: Economic Essays on Value, Competition and Utility. Cambridge University Press, London.
• Pasinetti, L. L., 1977. Lectures on the theory of production. Columbia University Press, New York.
• Pasinetti, L. L., 1980. The notion of vertical integration in economic analysis. In: Pasinetti, L. L. (Ed.), Essays on the theory of joint production. Cambridge University Press, New York.
• Passmore, J., 1978. A Hundred Years of Philosophy. Penguin Books, London.
• Perelman, M., 1987. “Marx’s crises theory: scarcity,” Labour and finance. Praeger Publishers, Westport, CT.
• Pollock, W. J., 2004. “Wittgenstein on the standard metre.” Philosophical Investigations 27 (2), 148-157.
• Ricardo, D., 2005a. Absolute value and exchangeable value. In: Sraffa, P., Dobb, M. H. (Eds.), David Ricardo, the Works and Correspondence, Vol. 4 (Pamphlets and Papers 1815-1823). Liberty Fund, Indianapolis.
• Ricardo, D., 2005b. Letter to Trower, August 31, 1823. In: Sraffa, P., Dobb, M. H. (Eds.), The Works and Correspondence of David Ricardo. Vol. 9. Liberty Fund, Indianapolis.
• Ricardo, D., [1817] 1996. Principles of Political Economy and Taxation. Prometheus Books, New York.
• Roemer, J. E., 1982. A General Theory of Exploitation and Class. Harvard University Press, Cambridge, Massachusetts.
• Roncaglia, A., 2005. The Wealth of Ideas. Cambridge University Press, The Edinburgh Building, Cambridge
• Ryle, G., [1949] 1984. The Concept of Mind. University of Chicago Press, Chicago.
• Samuelson, P. A., 1971. Understanding the Marxian notion of exploitation: A summary of the so-called transformation problem between Marxian values and competitive prices. Journal of Economic Literature 9 (2), 399-431.
• Seton, E, 1957. “The ‘transformation problem’.” Review of Economic Studies 24, 149-160.
• Sloman, A., 1978. The Computer Revolution in Philosophy: Philosophy, science and models of mind. Harvester Press and Humanities Press. [web]
• Smith, A., [1776] 1994. The Wealth of Nations. The Modern Library, New York.
• Sraffa, P., 1960. Production of commodities by means of commodities. Cambridge University Press, Cambridge.
• Steedman, I., 1981. Marx after Sraffa. Verso, London.
• Trigg, A. B., 2006. Marxian Reproduction Schema. Routledge, London and New York.
• Vickers, D., 1987. Money capital in the theory of the firm: a preliminary analysis. University of Cambridge, Cambridge.
• von Bortkiewicz, I., [1907] 1975. “On the correction of Marx’s fundamental theoretical construction in the third volume of Capital.” In: Sweezy, P. M. (Ed.), Karl Marx and the Close of his System. Augustus M. Kelley, Clifton, New Jersey, pp. 199-221.
• Wittgenstein, L., 1953. Philosophical Investigations. Blackwell, Oxford.